Geogebra Labs!
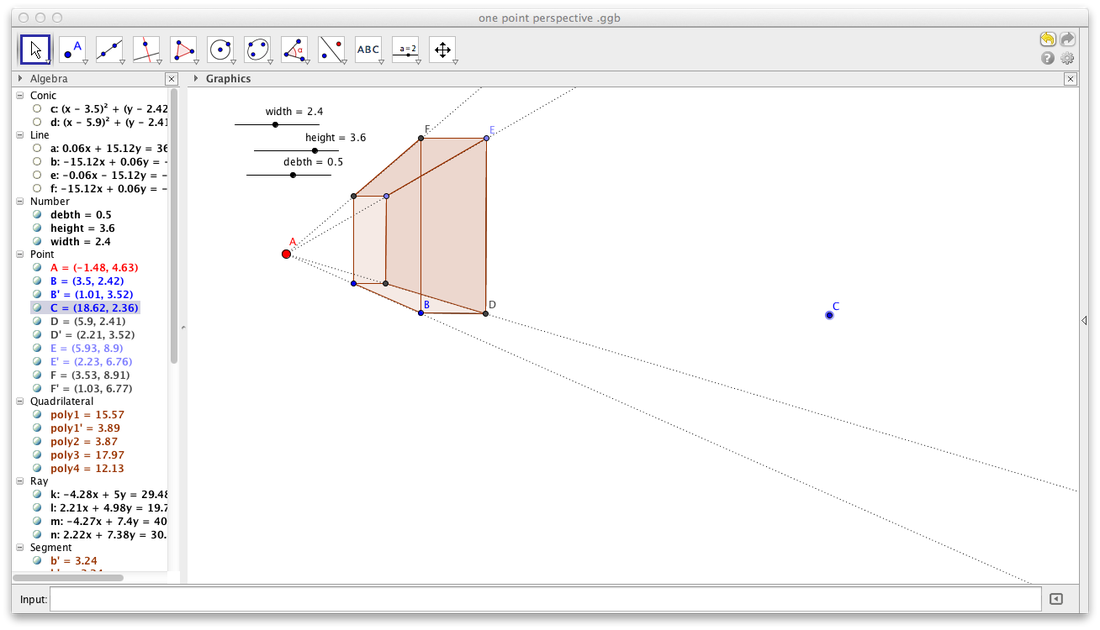
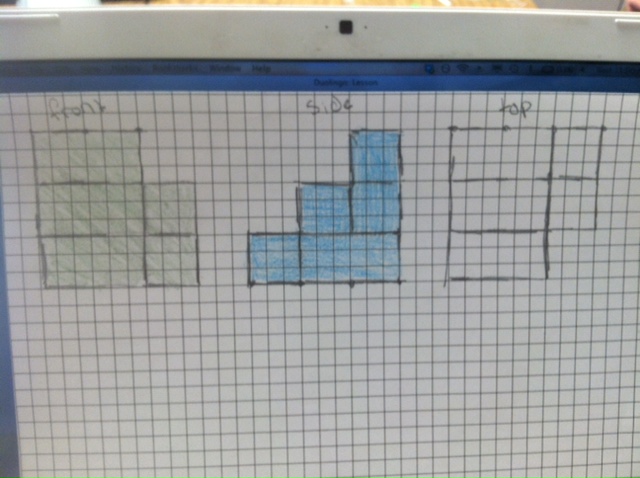
Orthographic Drawings!
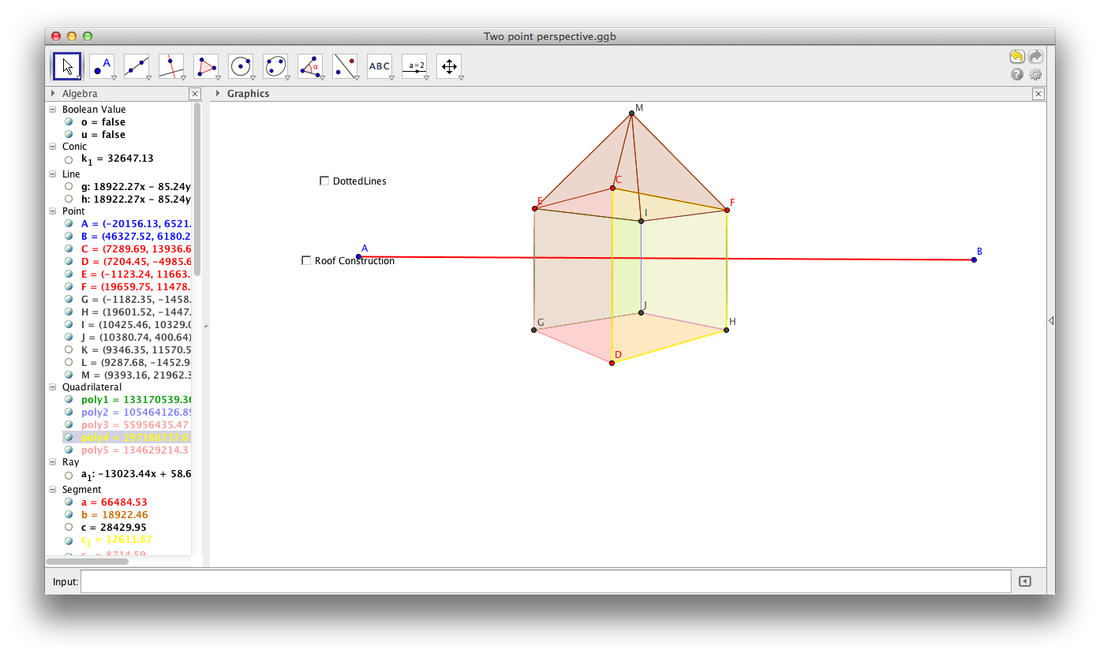
Anamorphic Drawings!
|
Definition
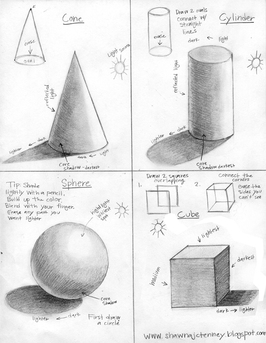
Something that is anamorphic is a shape or drawing that appears 3 dimensional due to unequal magnifications and shading on different parts of the object. As you can see in the pictures by drawing lines of different lengths and shading darker in some places as if there is a source of light makes the objects look anamorphic. Creation of Our Anamorphic Drawing To create the anamorphic drawing you see below my partner and I used a picture frame, a card board box, a poster board, a laser pointer, some paint, and a black sharpie. |
In order to get the picture you see on the picture frame onto the poster board we had one partner sit behind a desk and look through the picture frame with one eye so that the image on the picture frame would project itself onto the board. The person looking through the glass would also have a laser pointer and would point out key points of the picture to the other partner. The other partner puts marker, beads, on the board and then later connects the markers to create the image. Because this was a projection the final product is elongated in comparison with the original picture. When transferring something small into something big in matter of projection from the angle we did more focus is put on the upper half making the upper half bigger and the lower half smaller.
In order to get the picture you see on the picture frame onto the poster board we had one partner sit behind a desk and look through the picture frame with one eye so that the image on the picture frame would project itself onto the board. The person looking through the glass would also have a laser pointer and would point out key points of the picture to the other partner. The other partner puts marker, beads, on the board and then later connects the markers to create the image. Because this was a projection the final product is elongated in comparison with the original picture. When transferring something small into something big in matter of projection from the angle we did more focus is put on the upper half making the upper half bigger and the lower half smaller.
In order to get the picture you see on the picture frame onto the poster board we had one partner sit behind a desk and look through the picture frame with one eye so that the image on the picture frame would project itself onto the board. The person looking through the glass would also have a laser pointer and would point out key points of the picture to the other partner. The other partner puts marker, beads, on the board and then later connects the markers to create the image. Because this was a projection the final product is elongated in comparison with the original picture. When transferring something small into something big in matter of projection from the angle we did more focus is put on the upper half making the upper half bigger and the lower half smaller.
Finding Hight's Using Trig!
East Tree!
Calculations!
h=20tan16+xtan16
h=xtan21
x(tan16-tan21)= 20tan16
h=46.788mt
h=20tan16+xtan16
h=xtan21
x(tan16-tan21)= 20tan16
h=46.788mt
South Tree!
Calculations!
h=41tan8+xtan8
h=xtan7
x(tan7-xtan8)=41tan8
h=14.658my
h=41tan8+xtan8
h=xtan7
x(tan7-xtan8)=41tan8
h=14.658my
West Rock Spire!
Calculations!
h=15tan20+xtan20
h=xtan24
x(tan24-tan20)=15tan20
h= 15
h=15tan20+xtan20
h=xtan24
x(tan24-tan20)=15tan20
h= 15
Hexiflexigon
Brief Summary
My hexiflexigon designs use both rotational and line-reflection symmetry. The 2nd 3rd and 4th designs (Shown in the pictures above) all use rotational symmetry. The six triangles in these designs are 180 degree rotations of each other. There are however no lines of reflection. In the 1st design there is both rotational symmetry and line-reflection symmetry. there are line-reflections in between each of the 6 triangles, these triangle are also 180 degree rotations.
My hexiflexigon designs use both rotational and line-reflection symmetry. The 2nd 3rd and 4th designs (Shown in the pictures above) all use rotational symmetry. The six triangles in these designs are 180 degree rotations of each other. There are however no lines of reflection. In the 1st design there is both rotational symmetry and line-reflection symmetry. there are line-reflections in between each of the 6 triangles, these triangle are also 180 degree rotations.
Brief Reflection
I find the my first design the most pleasing. Due to the fact that it has both rotational and line-reflection symmetry I think it is better for understanding the geometrical concepts then the other three designs. Now that I better understand line-reflection symmetry and rotational symmetry if I where to make another hexiflexigon I would add more variety to my designs, I would make at one more design with both types of symmetry and one design with only line-reflection symmetry. I learned that I need to take better care of my school projects because I lost my first attempt at the hexiflexigon and had to redo it.
I find the my first design the most pleasing. Due to the fact that it has both rotational and line-reflection symmetry I think it is better for understanding the geometrical concepts then the other three designs. Now that I better understand line-reflection symmetry and rotational symmetry if I where to make another hexiflexigon I would add more variety to my designs, I would make at one more design with both types of symmetry and one design with only line-reflection symmetry. I learned that I need to take better care of my school projects because I lost my first attempt at the hexiflexigon and had to redo it.
Snail Trail Graffiti GGB Lab
Brief Summary and Reflection
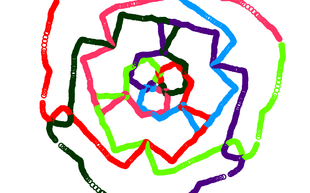
The snail trail graffiti lab taught us about several geometrical concepts and helped us learn more about geogebra. The geometrical concepts used in creating the work of art displayed above are rotations and reflections. Each one of the colors used in the design are traces of dots that are all reflections of one original dot, the green one. In order to reflect these dots you need something to reflect across, thats where the rotations come in to place. Each dot was reflected across a line which had been rotated 60 degrees. As well as learning about geometrical concepts I also learned a little bit about how these different concepts can be used. Before doing this and other geogebra labs all the concepts were separate, incorporating what we have learned about math into something beautiful helped me to realize why learning geometry is important.
The snail trail graffiti lab taught us about several geometrical concepts and helped us learn more about geogebra. The geometrical concepts used in creating the work of art displayed above are rotations and reflections. Each one of the colors used in the design are traces of dots that are all reflections of one original dot, the green one. In order to reflect these dots you need something to reflect across, thats where the rotations come in to place. Each dot was reflected across a line which had been rotated 60 degrees. As well as learning about geometrical concepts I also learned a little bit about how these different concepts can be used. Before doing this and other geogebra labs all the concepts were separate, incorporating what we have learned about math into something beautiful helped me to realize why learning geometry is important.
Two River GGB Lab
Summary of lab
There is a sewage treatment plant at the point where two rivers meet. You want to build a house near the two rivers (upstream from the sewage plant, naturally), but you want the house to be at least 5 miles from the sewage plant. You visit each of the rivers to go fishing about the same number of times but being lazy, you want to minimize the amount of walking you do. You want the sum of the distances from your house to the two rivers to be minimal, that is, the smallest distance.
There is a sewage treatment plant at the point where two rivers meet. You want to build a house near the two rivers (upstream from the sewage plant, naturally), but you want the house to be at least 5 miles from the sewage plant. You visit each of the rivers to go fishing about the same number of times but being lazy, you want to minimize the amount of walking you do. You want the sum of the distances from your house to the two rivers to be minimal, that is, the smallest distance.

You would not want to place your house here because it is too close to the sewage plant. Although it will be a shorter walking distance to the east river you wouldn't want to fish there because how close it is to the sewage plant. It would also not fit the requirements because it does not minimize the walking distance to both rivers.
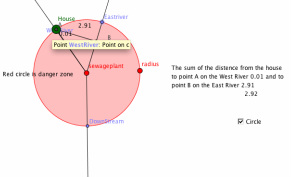
You would put your house here because there is a minimum and close to equal walking distance too both rivers. The house and both fishing places are also a good distance away from the sewage plant.
Burning Tent GGB Lab
Summary of Lab
A camper out for a hike is returning to her campsite. The shortest distance between her and her campsite is along a straight line, but as she approaches her campsite, she sees that her tent is on fire! She must run to the river to fill her canteen, and then run to her tent to put out the fire. What is the shortest path she can take?
A camper out for a hike is returning to her campsite. The shortest distance between her and her campsite is along a straight line, but as she approaches her campsite, she sees that her tent is on fire! She must run to the river to fill her canteen, and then run to her tent to put out the fire. What is the shortest path she can take?
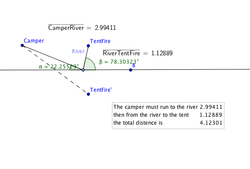
This would not be the quickest way to get from the river to the tent fire. Although it may look like a shorter distance in the image it actually is not. Because the distances from the camper to the river and from the river to the tent are not the same you would actually have to cover more distance in order to put out the fire.

This would be the fastest way to get from the river to the tent fire. The distances from camper to river and from river to fire are relatively the same and when the two distances are added they equal a smaller distance than in the previous picture.